Caracterização e mitigação de vibrações em tirantes e pontes

• 20 fevereiro 2015, sexta-feira
• EstruturasEstruturas Metálicas

Introduzidas, no seu conceito atual, após a Segunda Guerra Mundial, as pontes atirantadas têm sido crescentemente utilizadas em todo o mundo. Potenciadas pela introdução dos aços de alta resistência e pelos desenvolvimentos dos meios computacionais das últimas décadas, estas estruturas permitem

uma otimização da sua forma e do consumo de materiais e têm vindo a ser construídas em vãos crescentes. Com efeito, se inicialmente esta tipologia estrutural foi considerada a mais económica para vãos de 200 m a 500 m, a sua utilização tem sido igualmente estendida a pequenos vãos, particularmente de pontes pedonais, e a muito grandes vãos, de que se destaca a ponte da ilha Russky, com um tramo central de 1104 m, efetuando a ligação à ilha Russky da cidade de Vladivostok, na Rússia. Apesar de, quando comparadas com as pontes suspensas, as pontes atirantadas apresentarem menor flexibilidade, estas estruturas são também, e cada vez mais frequentemente, muito esbeltas e caracterizadas por baixos níveis de amortecimento, em particular dos seus tirantes, o que os torna suscetíveis às vibrações induzidas pelo vento e chuva e por outras ações operacionais. Por esta razão, a crescente construção destas estruturas tem sido acompanhada por reportes também crescentes de problemas de vibração dos tirantes, por vezes simultâneas com vibrações do tabuleiro e/ou torres.

As vibrações nos tirantes de pontes manifestam-se de forma distinta, nomeadamente envolvendo baixas amplitudes e frequências elevadas, ou então muito elevadas amplitudes e frequências baixas. Note-se que, mesmo nas situações de ocorrência de grandes amplitudes de vibração, não está em causa, normalmente, a resistência dos tirantes, já que os níveis de tensão induzidos por tais oscilações são muito baixos. Contudo, as elevadas amplitudes de vibração podem originar danos nos elementos de ligação, especificamente pelo impacto dos tirantes nos tubos de desvio, ou nos guardacorpos. Podem ocorrer, também, danos por fadiga nos cordões, decorrentes dos efeitos de flexão locais gerados nessas vibrações ou ainda a queda de tubos de revestimento. As elevadas amplitudes de oscilação poderão ainda originar a fendilhação do “grouting”, quando este seja usado, ou dos próprios tubos de polietileno, criando caminhos à propagação de humidade e ao aparecimento de danos por corrosão.

Neste contexto, é da maior relevância que o projeto de uma ponte atirantada incorpore uma componente de caracterização de potenciais vibrações dos tirantes, adotando medidas com vista à sua prevenção ou mitigação.

A complexidade do problema não permite, na presente data, identificar uma metodologia consolidada para a caracterização de vibrações em tirantes e para a mitigação dos seus efeitos. Contudo, há um conjunto de regras práticas e de análises simplificadas que se podem desenvolver e se passa a sistematizar. Numa primeira abordagem, importa claramente identificar os diferentes fenómenos de vibrações dos tirantes, que se podem classificar em duas categorias: as vibrações diretas, induzidas pelo vento e chuva; e as vibrações indiretas, decorrentes da oscilação das ancoragens.

VIBRAÇÕES INDUZIDAS PELA AÇÃO DIRETA DO VENTO E DA CHUVA

Incluem-se nesta categoria as vibrações induzidas pela ação turbulenta do vento. Estas vibrações decorrem das forças geradas pelo escoamento do ar em torno dos tirantes, as quais crescem com a velocidade média do vento, com o diâmetro do tirante e com a sua rugosidade. Nesse sentido, há clara vantagem na utilização de soluções compactas, em termos de dimensões, e de superfícies dos tubos de revestimento aerodinamicamente estudadas, o que constitui uma preocupação atual dos fabricantes. Por outro lado, é sabido que o amortecimento intrínseco dos tirantes é extremamente baixo, situando-se no intervalo de 0.05% a 0.5% para a generalidade das aplicações [1], sendo que o seu valor reduz com o aumento do comprimento do tirante. Contudo, este amortecimento vem acrescido do amortecimento aerodinâmico em situação de ocorrência de vento, o qual cresce também com a velocidade do vento. Daí que a situação mais crítica do ponto de vista das amplitudes de vibração devidas à ação turbulenta do vento decorra em situação de serviço, para a qual a resposta do tirante deverá ser caracterizada [2], devendo prever-se em particular medidas que evitem o choque entre tirantes adjacentes ou entre cabos estabilizadores [3].

Um segundo mecanismo de vibração dos tirantes ocorre em consequência da formação de vórtices na esteira do escoamento em torno do tirante. Estes vórtices são libertados alternadamente na face superior e inferior deste último, com uma frequência fv definida por

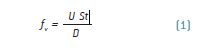
em que D representa o diâmetro exterior do tirante, U é a velocidade média do vento e St representa o número de Strouhal do escoamento, com um valor aproximado de 0.2 no caso de secções circulares. No caso de a frequência de libertação de vórtices se aproximar de uma frequência própria de um tirante, ocorre um efeito ressonante, de que resulta o chamado “lock-in”, ou sincronização. Este fenómeno caracteriza-se por uma oscilação do tirante nessa frequência num certo intervalo de velocidades de vento. Portanto, o “lock-in” pode ser caracterizado como uma instabilidade aeroelástica que ocorre para certos intervalos de velocidades críticas de vento Ucr definidas pelos harmónicos do tirante de acordo com a expressão  1).

Tendo em conta os valores dos diâmetros correntes dos tirantes, a análise de (1) permite concluir que as vibrações por “lock-in” acontecem para os modos de ordem elevada dos tirantes, já que as velocidades críticas para os modos de ordem mais baixa não são suficientes para induzir vibrações percetíveis. Considerando, por exemplo, uma velocidade crítica de vento de 10 m/s e um diâmetro de 0,20 m, o fenómeno de lock-in” ocorreria para uma frequência natural de 10 Hz. São mais vulneráveis ao fenómeno de “lock-in” os tirantes mais curtos, que exibem frequências naturais mais elevadas. Por outro lado, as elevadas frequências naturais envolvidas resultam também em amplitudes de vibração muito baixas, que não excedem normalmente 0.5 D.

O galope é um fenómeno de instabilidade aeroelástica típico de secções transversais não simétricas, caracterizado por muito elevadas amplitudes de oscilação, que podem exceder 10D. Este fenómeno ocorre para uma velocidade de vento acima de um valor crítico Ucr em qualquer frequência, resultando de um amortecimento aerodinâmico negativo  decorrente da oscilação do próprio tirante. De acordo com o manual do PTI [4], a velocidade crítica reduzida de vento Ucr, é determinada através de

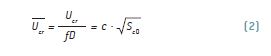
em que f representa a frequência natural do tirante, Sc0 representa o número de Scruton, definido por Sc0 = x m / (r D2) (x é o fator de amortecimento e m a massa distribuída por unidade de comprimento do tirante) e c é uma constante, de valor igual a 40, ou 35, de acordo com diferentes autores. A fórmula (2) permite então fixar um fator de amortecimento mínimo do tirante de modo a que a velocidade crítica para o galope seja superior à velocidade de projeto, com uma margem típica de 25%.

As características do fenómeno de galope permitem concluir que este fenómeno não ocorreria em tirantes com secções circulares, a menos que a sua forma fosse alterada, nomeadamente pela presença de gelo, ou então de um regato de água. Na realidade, a formação deste último, associada à combinação de chuva com vento, está na origem de uma das formas mais correntes de galope em tirantes de pontes, manifestando-se tipicamente para velocidades de vento intermédias, no intervalo de 8 – 12 m/s, com uma direção dominante de 20° a 60° com o eixo da ponte e intensidade de chuva fraca a moderada, em  tirantes com inclinações de 20° a 45° com o plano do tabuleiro, com diâmetros de 80 mm a 200 mm e para amortecimentos muito baixos, inferiores a 0.15%.

As vibrações por “lock-in” e galope podem ocorrer, igualmente, em associações de tirantes, em consequência de fenómenos de interferência motivados pela modificação do escoamento do ar na vizinhança de um tirante. Esta interferência aerodinâmica acontece habitualmente para distâncias entre tirantes inferiores a 4D, mas pode acontecer igualmente para afastamentos superiores, entre 8D e 20D. Neste sentido, e na eventualidade de ser necessária a ancoragem de tirantes em pares ou em associações múltiplas, deverão prever-se medidas de mitigação de potenciais vibrações.

VIBRAÇÕES INDUZIDAS PELA OSCILAÇÃO DAS ANCORAGENS

A atuação do tabuleiro e torres de uma ponte por ações de caráter dinâmico, como as induzidas por peões em pontes pedonais ou pelo tráfego rodoviário e ferroviário, podem suscitar vibrações destes elementos. A proximidade da frequência de oscilação do tabuleiro/ torres de uma frequência natural de um tirante poderá originar um fenómeno de ressonância interna, que se traduz na amplificação da oscilação do tirante. Atendendo a que as pontes atirantadas apresentam um grande número de tirantes com características muito semelhantes e, portanto, com frequências naturais muito próximas, a oscilação de um tirante poderá originar vibrações noutros tirantes próximos.

Em estruturas com baixos níveis de amortecimento, estas oscilações poderão ocasionar a amplificação das oscilações no tabuleiro/ torres, com a consequência de amplificarem ainda mais a vibração de um ou mais tirantes. Designa-se por excitação paramétrica o fenómeno de oscilação dos tirantes induzido por oscilação das suas ancoragens em frequências múltiplas ou sub-múltiplas da sua frequência natural. O fenómeno mais crítico do ponto de vista de suscetibilidade de um tirante corresponde à excitação de um tirante por oscilação da ancoragem na direção longitudinal com frequência dupla da frequência fundamental.

MITIGAÇÃO DE VIBRAÇÕES EM TIRANTES

Qualquer dos fenómenos e vibração anteriormente descrito está normalmente associado a níveis de amortecimento muito baixos, sendo que a sua ocorrência em geral não se manifesta quando o amortecimento mínimo dos tirantes é da ordem de 0,7% ou superior [1]. Assim, uma forma de claramente garantir a não-ocorrência de vibrações de tirantes, consiste no dimensionamento de amortecedores a inserir nos tubos de desvio dos tirantes ou então a colocar externamente (Fig. 1). O dimensionamento das características destes dispositivos é efetuado tendo por base a localização possível do amortecedor, a qual, habitualmente, não excede uma distância à ancoragem superior a 2% do comprimento da corda. De acordo com a metodologia apresentada em [2], o fator de amortecimento teórico máximo para um amortecedor viscoso linear é da ordem de 50% da distância relativa à ancoragem. Daí que, tendo em conta o valor acima fixado, e considerando ainda uma eficiência efetiva da ordem de 50%, se possa afirmar que o nível máximo de amortecimento conferido por um único amortecedor viscoso seja da ordem de 0,5%. Na realidade, em tirantes de grande comprimento, a posição do amortecedor dificilmente excederá 1% do comprimento da corda, do que resulta um amortecimento máximo de 0,25%. A combinação de amortecedores nas duas ancoragens permite obter um acréscimo de amortecimento próximo do acréscimo de amortecimento proporcionado por cada um dos amortecedores quando colocado isoladamente. Se em pontes de vãos intermédios, como a ponte Vasco da Gama, estas soluções são suficientes, nas muito grandes pontes poderá ser necessário o complemento com outras medidas, como por exemplo a utilização de cabos estabilizadores (Fig. 2).

Por fim, refere-se uma medida de caráter aerodinâmico que tem vindo a ser implementada na  generalidade dos tirantes de pontes, e que consiste na utilização de indentações ou nervuras na superfície externa das tubos de polietileno (Fig. 3), com a finalidade de impedir a formação de regatos de água e, desta forma, evitar as vibrações induzidas pela ação combinada do vento e a chuva.

REFERÊNCIAS

[1] CAETANO, E. (2007) - “Cable Vibrations in Cable-Stayed Bridges”, Structural Engineering Documents SED 9, ISBN 978-3-85748-115-4, IABSE

 [2] TABATABAI, H. & MEHRABI, A., 2000. Design of Mechanical Viscous Dampers for Stay Cables, Journal of Bridge Engineering, ASCE, Vol. 5, No.2, 114-123.

[3] SETRA, 2002. Cable Stays. Recommendations of French Interministerial Commission on Prestressing.

[4] PTI Guide Specification, 2007. Recommendations for Stay Cable Design, Testing and Installation. PTI